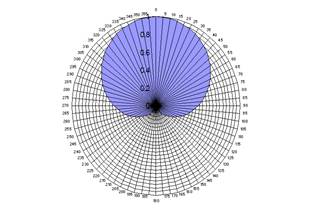
The theoretical response of a cardioid microphone

 The shuffling technique selected here is an entirely new technique and is intended to compensate for various shortcomings in crossed-cardioid recordings which are usually accused of lacking "spaciousness".
The shuffling technique selected here is an entirely new technique and is intended to compensate for various shortcomings in crossed-cardioid recordings which are usually accused of lacking "spaciousness".
In order to address the limitation noted in relation to crossed, velocity microphones and their characteristic of encoding the entire 360° soundstage, recording engineers have developed versions of the coincident microphone technique using cardioids which, by their nature, reject sound from the rear of the capsules. In usual deployments, the microphones are rigged on sturdy stands about two metres or more above the performance area floor and pointing slightly down. But to what extent is the response pattern of the cardioid microphone suitable for accurate stereo encoding?

The theoretical response of a cardioid is given by ½ (1 + cos θ) where θ is the angle of incidence of the sound wave. This curve is plotted above, and the curves for two, superimposed cardioid responses at ninety degrees to one another are plotted below.
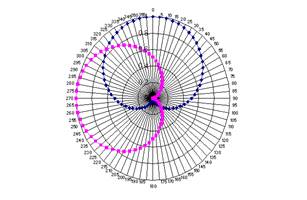
The curves are translated from polar form to rectangular form below (upper curves).
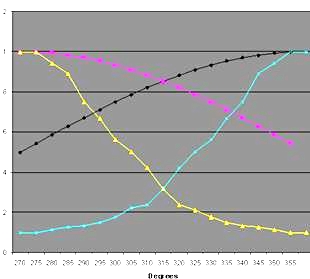
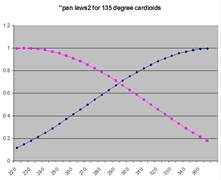
One way out of this impasse is to arrange cardioids at an angle greater than 90 degrees with respect to one another, as is illustrated above. This has the advantage that adequate inter-channel ratio is provided, but the microphones are so widely set that the stereo image is badly compressed laterally.
From the above we can conclude that crossed cardioids will provide insufficient level differences to provide correct stereo reproduction over loudspeakers at low and middle frequencies (<1kHz). This fact alone accounts for the lack of "spaciousness" or "low-frequency bloom" so often attributed to this microphone arrangement. It is also incorrect to refer to crossed-cardioids as "Blumlein technique" since he never - and surely never would have - endorsed such an approach.
It may seem incredible given this consideration that this technique works at all. In fact, as shown above, the only reason the crossed-cardioid technique gives reasonable results is due to the HF "beaming" which the microphones normally possess which ensures the exaggerated high-frequency channel differences predominate over the mono signal at higher frequencies.
This may seem like a damning indictment of the crossed-cardioid microphone technique. However, it suggests a manner in which the signals might be improved by the addition of a mono, omnidirectional microphone signal fed in anti-phase to the left and right signals; thereby cancelling the unwanted mono component in the cardioid signals. This would work like this,
A = (½ + ½ cosθ) - ½ = ½ cosθ
In words: if an anti-phase, omni response is added (-6dB) to the output from one of the microphones, the resultant is a cosine response of reduced sensitivity.
Whilst it might prove an interesting experiment to attempt to use three microphones in an array of this sort, the practicalities of finding microphones with matching responses would be a real challenge and the possible phase cancellation effects that such a technique might induce could prove problematic. (Nevertheless, there's a fun post-grad' project awaiting someone here!)
In any case, a simpler electronic solution exists: it is to reduce the gain common-mode signal in relation to the differential-mode signal. (The common-mode signal being the components of the left and right signals which are common, i.e. MONO: and the differential-mode signals being the STEREO information.)
Such a process is at the heart of this algorithm which processes the signals from a coincident cardioid stereo pair to tease out the velocity response of the pair from the unwanted, mono, "coincident-omni" response. But there's a complication. This omnidirectional, subtraction process must only happen at low-frequencies. At HF, the microphone beaming effects will provide the differential-intensity stereo information.
 Home page
Home page
For all support issues, go here.
For Pspatial Audio sales, email: sales@pspatialaudio.com
